Makine Öğrenmesi 6 - Markov Zinciri Monte Carlo Algoritması
15 Mar 2020
Reading time ~17 minutes
Emre: Markov Zinciri Monte Carlo yöntemi genetikten GPS konumlamaya; nükleer silah araştırmaları, RADAR ve robotik çalışmalarından finansal tahminleme işlerine kadar makine öğrenmesine ihtiyaç duyulan her alanda kullanılıyor.
Matematiksel ispatlara girmeden Markov Zinciri Monte Carlo (MZMC)’nun mantığını anlatabilir misin? MZMC neden bu kadar önemli.
Kaan: Elbette. Herşeyden önce bu Monte Carlo fikri nereden ortaya çıktıdan başlayabiliriz.
Problem: Ya sonsal dağılımı analitik yollarla hesaplayamıyorsak?
Kalman filtresi bahsinde sonsal dağılımı analitik olarak hesaplayabilmiştik. Ancak her zaman o kadar şanslı olmayabiliriz. Dinamik - zamanla değişen - ve doğrusal olmayan sistemlerde, hele de dağılım Gaussian da değilse sonsal dağılımı analitik olarak hesaplayamayabileceğimizden ve bu durumda Monte Carlo yöntemi gibi ileri teknikler kullanıldığından bahsetmiştim. Üzerine bir de modelimizde yüzlerce ve hatta binlerce parametre varsa, integral daha da içinden çıkılmaz hale geliyor.
Emre: Sonsal dağılım neden analitik olarak hesaplanamıyor?
Kaan: Bayes kuralını hatırlayalım:
\[P(\theta|x) = \frac{P(x|\theta) P(\theta)}{P(x)}\]$P(\theta|x)$, elimizde $x$ gözlemleri varken bize model parametrelerimizin olasılık dağılımını veriyordu. Bulmak istediğimiz sonsal dağılım bu dağılım. Ancak bunu hesaplayabilmek için $P(\theta)$ öncül dağılımı (gözlemler henüz elimize geçmeden önce parametreler hakkındaki ön bilgilerimizden varsaydığımız dağılım) ile $P(x|\theta)$ olabilirlik dağılımını (parametreler hakkında herşeyi bildiğimiz durumda gözlemlerin dağılımı) çarpıyoruz. İşin bu kısmı kolay.
Bir de paydaya bakalım. $P(x)$ neydi?
Emre: Kanıt. Yani parametrelerden bağımsız bir şekilde $x$ gözlemlerinin bu modelden gelme olasılığı.
Kaan: Aynen. Yani burada $\theta$ üzerinden bir marjinalleştirmeye ihtiyaç var. Bir diğer ifadeyle $x$’i yalnız bırakmak için $\theta$’nın mümkün olan tüm değerleri üzerinden bir integral almamız gerekiyor.
\[Z = P(x) = \int_{\Theta}^{} p(Y|X,\theta)p(\theta)d\theta\]Bu integral sonunda sonuçta ortaya bir normalizasyon sabiti $Z$ çıkıyordu hatırlarsan. Elimizdeki sonsal dağılımın olasılık değerlerinin $0$ ile $1$ arasında değiştiğinden emin olmak için bu normalizasyon işlemine ihtiyacımız var.
Peki ya bu integrali analitik olarak kapalı formda bulamıyorsak?
Emre: Yaklaşık olarak bulmaya çalışabiliriz.
Kaan: Makul. Bulmaya çalıştığımız sonsal dağılımdan örnekler çekebilseydik belki Monte Carlo simülasyonu ile yaklaşık bir sonuç bulabilirdik ama bu da bize yetmezdi çünkü bunu yapmak için bile Bayes formülünü çözmemiz bir de örnek çekebilmek için dağılımın tersini hesaplamamız gerekirdi ki bu daha da zor olacaktır.
İşte burada sahneye Markov Zinciri Monte Carlo algoritması çıkıyor ki, basitçe söylemek gerekirse MZMC yukarıda sözü geçen integrali hesaplamaya gerek kalmadan ve sonsal dağılımı analitik olarak çözmeden sonsal dağılımdan örnekler çekmemizi sağlıyor. Böylece bu örnekler üzerinden sonsal dağılımın beklenen değerini hesaplayabiliriz!
Markov Zinciri Monte Carlo
MZMC üç ana bileşenden oluşur.
- Monte Carlo (MC) yaklaşık çözümü
- Markov Zinciri (MZ)
- Metropolis-Hastings (MH) algoritması
Monte Carlo Yaklaşık Çözümü
Genel olarak Monte Carlo yönteminin kullanım alanı, hesaplanması zor olasılıkların tahmini; karmaşık sistemlerin sonucunda oluşan parametrelerin tahmini; test istatistikleri için kritik degerlerin elde edilmesi; hesaplanması zor olan integrallerin tahmini vb. diyebiliriz. Örnegin; dagılımını ifade edemediğimiz bir istatistiğin beklenen değerini Monte Carlo yöntemi ile tahmin edebiliriz. Bilinen bir dagılıma sahip olmayan ya da dağılımı bilinmeyen bir istatistiğe ait kritik değerleri elde etmekte Monte Carlo yöntemini kullanabiliriz. Bazı varsayımlardan sapmalar olduğunda istatistiklerin davranışlarını yine Monte Carlo yöntemi ile inceleyebiliriz. Daha net bir ifadeyle; analitik olarak çözümleyemedigimiz olayları incelemek için Monte Carlo yönteminin kullanılabileceğini söyleyebiliriz.
Monte Carlo yaklaşımının erken varyantı 18. yüzyılda Buffon iğnesi probleminin ortaya atılması ile ortaya çıkmıştı. Buffon basit bir soru soruyordu “birbirine paralel çizgilerin arasına rasgele şekilde bir iğne atarsam, bu iğnenin çizgilerden en az birini kesme olasılığı nedir?” Lazzarini bu problemin çözümünü $\pi$ sayısını hesaplamak için olasılıksal bir metod olarak kullandı. Böylece çözüm yöntemi meşhur oldu.
Gerçi Lazzarini konusu biraz karışık. Lazzarini yaklaşık olarak bulduğu denklemle $\pi$ sayısını çok büyük hassasiyetle hesaplayabiliyor. Deneyde biraz değişiklik olduğundaysa çok büyük sapma olduğundan Lazzarini deneyi sonucu en iyi şekilde verecek sayılarla mı tasarladı diye olay tartışmaya açılıyor. Herneyse bu konumuzun dışında.
Sonraları Monte Carlo yönteminin ileri varyantları 1940 yılında Los Alamos Ulusal Laboratuarında nükleer silah araştırmalarında yeniden gündeme geldi. Algoritma popülerlik kazandıkça günümüzde genetikten GPS konumlamaya; RADAR, robotik çalışmalarından finansal tahminlere kadar her alanda kullanılmaya başladı.
Peki Monte Carlo yöntemini bu kadar özel ya da başarılı yapan şey neydi?
Monte Carlo yönteminin başarılı olmasının altında yatan sır aslında olasılık kuramından bildiğimiz Büyük Sayılar Yasası (BSY)’dır. Olasılık kuramında, BSY aynı deneyin büyük bir sayıda yinelenmesi sonucunu betimleyen bir teoremdir. BSY’na göre, büyük bir sayıdaki denemelerden elde edilen sonuç beklenen değere yakın olmalı, ve daha fazla deneme yapıldıkça daha da fazla yakın olma eğiliminde olmalıdır. Örneğin, rassal çıktıları olan bir süreci düşünelim. Rassal bir değişken defalarca gözlensin. O zaman gözlenen değerlerin ortalaması uzun dönemde kararlı olur. Dolayısı ile söz konusu bir rassal değişkenin beklenen değerini tahmin etmede en iyi yöntem, sayıca yeterince büyük bir örnek ortalamasını ilişkin olduğu beklenen değerin sapmasız tahmin edicisi olarak kullanmaktır. Temel fikir budur.
Sonuç olarak, MC bileşeni bir dağılımdan (ör; $\theta_t \sim \mathcal{N}(0.5, \sigma^2)$) örnekler çekmemizi ve bu örnekler üzerinden dağılımın beklenen değerini hesaplamamızı sağlar.
Unutma MC adımının bize sağladığı kazanç basit görünen ama ileride çok işlevsel olacak bu BSY varsayımı. Neden işe yaradığına geleceğim.
Önem Örneklemesi
Bir sonraki basamakta, Markov Zinciri Monte Carlo yoluna giden fikirler silsilesinde ortaya çıkan ilk fikirlerden biri “önem örneklemesi” fikridir(öncesi de var ama o kadar detaya girmeyeceğim).
Amacımız yukarıda sözü geçen integralini alamadığımız $P(x)$’i ya da diğer adıyla $Z$’yi yaklaşıkta olsa kestirebilmenin bir yolunu bulmak. Artık elimizde MC yaklaşımından gelen BSY fikri var. Bakalım üzerine daha ne koyabiliriz.
Bu fikrin özü de şudur; ne olduğunu bildiğimiz ve gerçekte üzerinde çalıştığımız sistemin sonsal dağılımına yakın olduğunu düşündüğümüz bir $q(\theta)$ dağılımı öneririz ve bu dağılımı şu şekilde kullanabiliriz:
\[Z = \int_{}^{} \dfrac{p(Y|\theta)p(\theta)\color{red}{q(\theta)}d\theta}{\color{red}{q(\theta)}}\]Sonuçta pay ve paydayı aynı şeye bölmek sonucu değiştirmez değil mi?
Bu durumda $Z$’yi şöyle yazabiliriz;
Yani artık $W$ burada $\theta$’nın bir fonksiyonudur. Mesela örnekleri $q(\theta) \sim \mathcal{N}{(0, 1000)}$ dağılımından çektiğimizi varsayalım, değerlerini yerine koyup $W$’yu hesaplayabiliriz. Burada yine yardımımıza BSY koşuyor. Büyük Sayılar Yasası bize;
\[Z \approx \frac{1}{N} \sum_{i=1}^{N} W(\theta^{(i)})\]olduğunu söyler. Bu şu demektir; eğer $W$ burada $\theta$’nın bir fonksiyonuysa, bu integral örneklerin ortalamasına denktir (bunun da ispatına girmeyeceğim).
Yani elimizdeki $q(\theta)$’dan gelen örnekleri kullanarak $Z$’i artık yaklaşık olarak hesaplayabiliriz. Güzel $Z$ yi yaklaşık olarak hesaplayabildiğimize göre sorun burada çözülmüş olmalı, değil mi?
Emre: Öyle olmadığı sorudan belli.
Kaan: Evet. Malesef sorun şu ki, bu $Z$ hesabıyla sonsal dağılıma ait histogramlar çizdirebilmek için $K$ boyutlu ($K$ rassal çok-değişkenkli) problemlerde tüm dağılımı hesaplayabilmek için $N^K$ örneğe ihtiyaç duyarız. Ki, $N$’nin bir milyon ve $K$’nin $25$ olduğu bir gerçek dünya probleminde ($10^{150}$ örnek gerekli) artık histogramlar ihtiyaç duyulan kısa sürelerde hesaplamayacak kadar ağır işlem yükü gerektirir. Buna boyutların laneti (curse of dimensionality) denilir.
Emre: Buradan da bir çıkış var değil mi?
Kaan: Elbette. Önerilen bir dağılımdan örnekler çekme bize yeni bir bakış açısı kazandırdı. Artık önerdiğimiz bir dağılımdan örnekler çekerek ve BSY’ını kullanarak kestirim yapmayı öğrendik. Ancak çok boyutlu tahmin problemlerini çözebilmek için histogramlar hesaplamak yerine olaya bambaşka bir açıdan bakmamız gerekiyor.
Histogramlar yerine tahmin dağılımları üzerinde çalışabiliriz.
Elimizde $Y_{1:t}$ geçmiş verisi varken, $X_{t+1}$ zamanına ait gelecek tahminimize ($Y_{t+1}$) ait olasılık dağılımını şöyle yazabiliriz:
\[P(Y_{t+1}|X_{t+1},Y_{1:t}) = \frac{1}{Z} \int_{}^{} P(Y_{t+1}|X_{t+1}, \theta) P(Y_{t+1}|\theta)P(\theta)d\theta\]$Z$’yi Monte Carlo Önem örneklemesiyle nasıl bulacağımızı biliyoruz. Ama bu kez bir farklılık daha yapmamız gerekecek.
Önem örneklemesini işe yarar hale getiren en önemli matematik hilelerinden birini yapıyoruz dikkat et!
Yine $W$ numarasını kullanacağız (yani bir $q(\theta)$ ile çarpıp yine $q(\theta)$’ya bölerek $W$’yu $\theta$’nun bir fonksiyonu haline getirme numarası) ancak bu kez ifadenin hem payına hem paydasına “aynı anda” Monte Carlo uygulayacağız!
O zaman da tahmin dağılımımızı şöyle ifade edebileceğiz:
\[P(Y_{t+1}|X_{t+1},D) = \sum_{i=1}^{N} \hat{w}(\theta^{(i)})P(Y_{t+1}|X_{t+1},\theta^{(i)})\]ki
\[\hat{w}^i = \frac{w^i}{\sum_{j}^{}w^j}\]diye tanımlanabilir. Burada yine histogram hesaplıyor gibiyiz ama bu kez ağırlıklar normalize ediliyor. Sonuçta hesapladığımız dağılımın integrali $1$’e eşit olacak. Yani olasılık dağılım fonksiyonu olmanın gerek şartını yerine getirmiş olacak.
Büyük bir atlama yaptık ileri doğru. Tahmin dağılımının ilk halinden buraya nasıl geldiğimizin çıkarımı burada yapılamayacak kadar uzun ve karmaşık.
Ama şöyle mantığını izah edeyim. Pay ve paydaya aynı anda Monte Carlo uygulayarak $Z$’den kurtulduk. Artık hesaplamak zorunda değiliz. Bu derivasyon Bayesçi çıkarımdaki en önemli derivasyondur. Bu konularda doktora çalışması yapmayı planlıyorsan bu çıkarımı mutlaka kendi kendine ispat etmelisin.
Artık devasa boyutlu verilerle histogram hesaplamaya gerek kalmadan tahmini sonsal dağılım hesabı yapabiliyoruz. Ancak, malesef, bu da tüm problemlerimizi çözmüyor.
Önem Örnekleme $5$-$10$ parametreli problemlerde (ör; biyoinformatik, lojistik regresyon) kullanılabilir. Önerdiğimiz $q(\theta)$’nın makul bir dağılım olduğunu varsayarsak ve önerdiğimiz dağılım $\theta$’nın beklenen değerini içinde bulundurduğu sürece bu yaklaşıma güvenebiliriz. Robotik problemlerinde (ör; kendi kendine evi süpüren elektrikli robotlar) Parçacık Filtreleme gibi Ardışık Önem Örneklemesi varyantı sıkça kullanılır.
Ancak tahmin edilecek parametre sayısı arttıkça önerdiğimiz $q(\theta)$ dağılımları artık gerçekçi olmaktan kaçınılmaz olarak çıkacaktır. Bu nedenle yüksek sayıda parametre olan durumlar için (ör; finansal tahminleme) başka bir çözüm bulunması gerekiyordu. Böylece Markov Zinciri Monte Carlo algoritması ortaya çıktı.
Markov Zinciri (MZ)
Markov zinciri $\theta$ durumunun yalnızca $\theta_{t-1}$’e koşullu olmasını sağlar. Yani eğer stokastik bir durum-uzay modelini Markov süreci olarak modellersen bir sistemin bir sonraki durumu kendisinden önceki tüm $\theta_{t-1, t-2, …, t-N}$ durumlarına değil yalnızca bir önceki $\theta_{t-1}$ durumuna koşulludur.
Yeni durumu şöyle ifade edebiliriz: $\theta_{t} \sim \mathcal{N}(\theta_{t-1}, \sigma^2)$.
Yani bir önceki rassal örneği dağılımın ortalama değeri olarak kullanarak yeni bir rassal örnek üretiriz. Bunu şu şekilde görselleştirebiliriz:
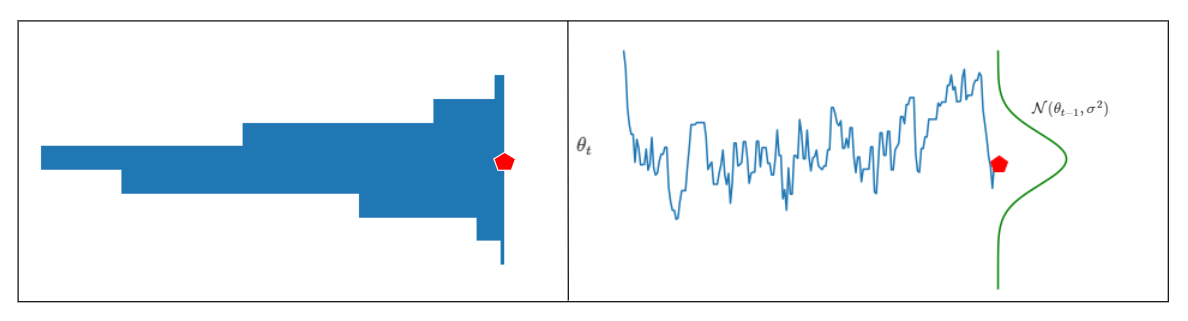
Bu figür bize ne anlatıyor?
Sağ tarafta üretilen her bir yeni örneğin kendisinden önceki örneği ortalama parametresi olarak alan bir Normal dağılımdan geldiğini görüyoruz. Soldaki histogram da üretilen rassal örneklerin histogramı. Dikkat edersen histogram sağdaki öneri dağılımına pek benzemiyor. Çünkü bu örnekler rasgele adımlarla (random-walk) üretildi.
Sonuç olarak yine de Markov zincirini kullanarak durağan (hatta ergodik) bir dağılımdan örnekler çekmeyi başarmış oluyoruz. Yine de çektiğimiz örneklerin dağılımı sonsal dağılıma (ya da öneri dağılımına) benzemiyor. Bu sorunu da Metropolis-Hastings algoritması çözecek.
Şunu söylemeden geçmeyeyim, burada Markov Zinciri’nin durağan bir dağılıma sahip olduğunu ve ergodik bir süreç olduğunu varsaydık. Bu zincirin sahip olması gereken bir sürü özellik var (indirgenebilirlik, dönemsellik ve tekrarlama ile ilgili)aslında. Bu nokta MZMC’nin can alıcı noktasıdır ve üzerine sayfalarca tartışılacak bir bahistir, o yüzden burada bana güvenip bu varsayımın işe yaradığını bilmeni istiyorum.
Emre: En azından “ergodik” ne demek?
Kaan: Markov Zinciri’ndeki durumların arasındaki geçişleri tanımlayan olasılık matrisine $T$ diyelim. $T$ geçiş matrisinde tüm durumlar birbirleri arasında geçiş sağlayabiliyorsa ve ortalama aldığımız süre (örnek sayısı yeterince çoksa) yeterince uzunsa bu zincire ergodik markov zinciri denir. Eğer ortalama aldığımız süre yeterince uzunsa, teorik olarak örnek ortalaması sinyalin gerçek ortalamasına yakınlaşır.
Metropolis-Hastings (MH) algoritması
Bu basamak öneri dağılımından Markov zincirine uyarak üretilen örneklerin hangilerini kabul edip hangilerini reddedeceğimizi belirler.
Önce Markov zincirinden henüz çekilen (mevcut) örneğin sonsal dağılımdan gelme olasılığı ile önceki örneğin sonsal dağılımdan gelme olasılığının oranını buluruz;
\[r=min\{1,\frac{önerilen \space örneğin \space olabilirliği \times önerilen \space örneğin \space öncül \space olasılığı}{ önceki \space örneğin \space olabilirliği \times önceki \space örneğin \space öncül \space olasılığı}\}\]Bu durumda $r=1$ ise önerilen örneği hemen kabul ediyoruz. Önerilen yeni örneğin sonsal dağılıma ait olma olasılığı bariz yüksek demektir. Ancak bu oran $1$’den küçükse burada bir seçim şansımız var.
Oran $1$’den küçükse, bu oranı düzgün dağılımdan, $U[0,1]$, rasgele seçtiğimiz bir sayıyla karşılaştırarak Markov zincirinden gelen yeni örneği kabul edip etmeyeceğimize karar veririz.
Eğer düzgün dağılımdan gelen sayı kabul etme olasılığımızdan ($r$ oranından) küçükse Markov zincirinden gelen örneği yeni örnek $x^{\star}$ olarak kabul ediyoruz, değilse de yeni örneğimiz bir öncekiyle aynı oluyor.
Bunu şöyle bir analojiyle açıklamaya çalışabilirim. Ortaya bir problem atıyorum ve aslında bu problemin elimde bir çözümü var. Ortaya sorduğum soruya bir yerden bir cevap geliyor. Eğer bu cevaptaki çözüm elimdekinden daha iyiyse yeni cevabı halihazırda çözüm olarak kabul ediyorum, değilse reddediyorum ve eski çözümü tutuyorum; emin değilsem de kabul edip etmemek konusunda zar atıyorum!
MZMC Algoritması
Bizi MZMC yöntemine getiren fikir silsilesine bir daha bakalım. Önce Monte Carlo yaklaşık çözümüne baktık. İntegralleri alamadığımız durumlar için büyük sayılar kuralından yararlanıp Önem örneklemesi yöntemini geliştirdik. Ancak histogram hesabının pahalı bir işlem olduğunu (yapay sinir ağlarında binlerce boyutlu değişkenler hesaplanıyor; boyut sayısı artınca bu yöntemde işlem yükü açısından makul olmaktan çıkıyor) gördük. Tahmin denklemleri üzerinden gitmeye karar verdik. $Z$’yi yaklaşık olarak bulmak yerine denklemin hem payı hem de paydasını aynı anda yaklaşık olarak hesaplayan ve $Z$’yi hesaplamaktan kurtulan Normalize edilmiş Önem örneklemesi yöntemine geçtik. Yine gördük ki bu yöntem de az sayıda parametreli problemler için işe yarıyor. Parametre sayısı arttıkça önerdiğimiz dağılımla ilgili varsayımlarımızın gerçekle olan bağlantısı azalıyor, gerçekçi olmaktan uzaklaşıyor. Bu nedenle çok parametre sayısında da işe yarayacak yeni bir yönteme ihtiyaç duyduk.
Şimdi MZMC’nin Metropolis-hastings algoritmasına ve ne kadar başarılı çalıştığına bakabiliriz.
$X$’in durum (durum-uzay modelindeki “durum”) vektörümüz ve $q$’nun da öneri dağılımı olduğunu varsayarak MZMC’nin algoritmasını şu şekilde yazabiliriz:
- adımda parametre vektörümüzü ilklendiriyoruz ve hedef dağılıma benzediğini düşündüğümüz öneri dağılımını seçiyoruz
- adımda bir döngü başlatıyoruz
- adımda $[0,1]$ aralığında düzgün $U$ dağılımından rasgele bir sayı çekiyoruz.
- adımda elimizdeki $x^{i}$ örneğini $q$ öneri dağılımından geçiriyoruz. Yani ortalaması $x^{i}$ olacak şekilde $q$’dan bir örnek çekiyoruz. Bunu şöyle de ifade edebiliriz; $x^{\star} = X^{(i)} + \mathcal{N}(0, \sigma^2)$. (Yeni örneğimiz bir öncekinin yakınında bir yerde çıkacak.)
- adımda yeni parametrenin sonsal dağılımı ile bir önceki parametrenin sonsal dağılımlarının oranını hesaplıyoruz. Bu oran bizim “kabul etme olasılığımızı” belirliyor. Ancak dikkat edersen $Z$’leri bilerek sadeleştirmeden yazdım. Aslında bu basamakta $Z$’ler sadeleşiyor, bu nedenle artık o malum integrali hesaplamamıza gerek kalmıyor!
- adımda düzgün dağılımdan çektiğimiz örnekle bu oranı karşılaştırıyoruz. Eğer düzgün dağılımdan gelen sayı kabul etme olasılığımızdan ($r$ oranından) küçükse Markov zincirinden gelen örneği yeni örnek $x^{\star}$ olarak kabul ediyoruz, değilse de yeni örneğimiz bir öncekiyle aynı oluyor.
- adımda döngünün sonuna gelip gelmediğimize bakıyoruz, gelmediysek sayacı artırıp 3. adıma geri dönüyoruz
Algoritmanın akışını şu şekilde görselleştirebiliriz:
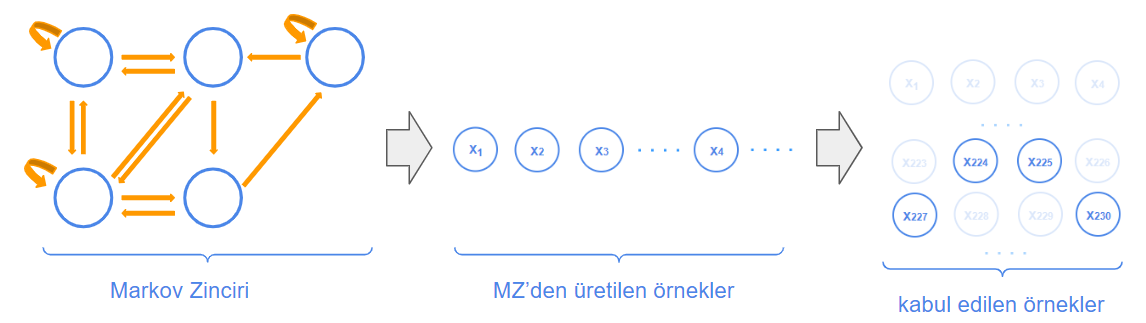
Soldaki şekil bize Markov Zinciri‘mizi gösteriyor.
MZMC’de ergodik olduğunu düşündüğümüz Markov Zinciri’inden gelen ve kriterimize uyan bazı örnekleri kabul ediyoruz. MZMC’nin bu seçimleri yaparak hedef dağılıma nasıl ulaştığını interaktif olarak görmek için The Markov-chain Monte Carlo Interactive Gallery‘ye bakabilirsin.
Algoritma Kodlama
Şimdi bir model tanımlamamız lazım. Basit olsun diye hedef dağılımın Normal dağılım (ör; olabilirlik dağılımı) olduğunu varsayalım. Normal dağılımın bildiğin üzere iki parametresi var. Biri $\mu$ ortalama, diğeri $\sigma$ standart sapma. Kolaylık olsun diye $\sigma=1$ kabul edelim ve $\mu$’nün sonsal dağılımı hakkında çıkarımda bulunmaya çalışalım. Çıkarım yapmaya çalıştığımız her parametre için bir de öncül dağılım varsaymamız lazım. Şimdilik kolaylık olsun diye bunu da Normal dağılım olarak varsayalım. Yani varsayımlarımız şu şekilde;
Ortalaması $0$ olan ve Normal dağılımdan gelen $20$ adet rassal gözlem üretelim. Bunların gerçek hayatta gözlemlediğimiz sistemden geldiğini düşünebilirsin.
import numpy as np
import pandas as pd
import scipy as sp
import matplotlib.pyplot as plt
from scipy.stats import norm
np.random.seed(225)
gozlem = np.random.randn(20)
plt.hist(gozlem, bins='auto')
plt.xlabel('gozlem')
plt.ylabel('gözlem sıklığı')
plt.show(
Ürettiğimiz rassal gözlemlerin histogramı aşağıdaki gibi olacaktır.
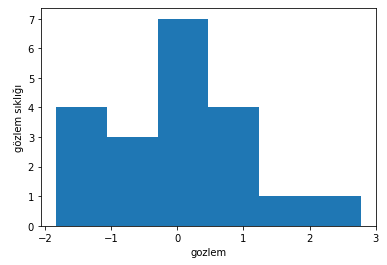
Bu modelin güzel tarafı şu ki artık sonsal dağılımı analitik olarak da hesaplayabiliriz. Standart sapması bilinen Normal dağılımlı bir olabilirlik varsa, bu durumda Normal dağılımlı bir $\mu$ konjuge öncül olacaktır (yani öncül dağılımla sonsal dağılım aynı olacak). Sonsal dağılımın parametrelerini nasıl hesaplayabileceğimizi wikipedia veya başka yerden bulabiliriz. Matematiksel çıkarımını şurada bulabilirsin.
Bakalım gözlemler elimizdeyken analitik olarak sonsal dağılım neye benziyor.
def sonsal_analitik_hesapla(gozlem, x, mu_ilk, sigma_ilk):
sigma = 1.
n = len(gozlem)
mu_sonsal = (mu_ilk / sigma_ilk**2 + gozlem.sum() / sigma**2) / (1. / sigma_ilk**2 + n / sigma**2)
sigma_sonsal = (1. / sigma_ilk**2 + n / sigma**2)**-1
return norm(mu_sonsal, np.sqrt(sigma_sonsal)).pdf(x)
x = np.linspace(-1, 1, 500)
sonsal_analitik = sonsal_analitik_hesapla(gozlem, x, 0., 1.)
plt.plot(x, sonsal_analitik)
plt.xlabel('mu')
plt.title('analitik sonsal dağılım')
plt.show()
Elimizdeki gözlemlere bakarak $\mu$’nün olasılık dağılımı (analitik olarak) şöyle görünüyor;
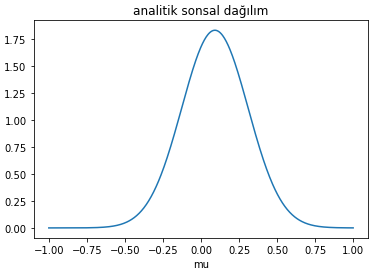
Gerçek hayatta bu kadar şanlı değiliz. Genellikle öncül dağılım konjuge olmaz ve sonsal dağılım da elle çıkarımı yapılacak kadar kolay bulunamaz. Öyleyse bu durumda MZMC algoritmasını devreye sokma vaktidir.
Algoritmanın ilk adımı dağılımını bulmak istediğimiz parametreyi ilklendirmekti. Bu bulmaya çalıştığımız parametre hakkında elimizdeki tüm bilgileri kullanarak yapabileceğimiz bir şey. Varsayalım ki bulmaya çalıştığımız $mu$ parametresinin $1$ civarında olacağına dair bir kanaatimiz var. Bunu $\mu = 1$ diye ilklendirerek kullanabiliriz.
Bu ilk noktadan başka bir noktaya atlamamız lazım (işin Markov bileşeni burada devreye giriyor). Ama nereye?
Bu konuda baya sofistike olabiliriz ya da aptalca davranabiliriz. Daha önce sözünü ettiğim Öneri dağılımına burada ihtiyacımız var. Bir sonraki noktaya bu öneri dağılımına göre atlayacağız. Bu anlamda Metropolis örnekleyicisi aslında aptaldır. Elimizde olan $\mu$ değerini merkeze alarak Normal dağılıma göre, ki bu Normal dağılımın biraz önce varsaydığımız model dağılımlarıyla ilgisi yok, yeni bir noktaya atlar. Ne kadar uzağa atlayabileceğimiz bu öneri dağılımının genişliğiyle (standart sapması) ilgilidir. Bir sonraki adımda ne yapıyorduk?
Emre: Geldiğimiz yeni noktayı kabul edip etmeyeceğimize bakıyoruz.
Kaan: Çok iyi.
Vardığımız noktadaki yeni Normal dağılım elimizdeki gözlemleri daha iyi açıklıyorsa bu yeni noktayı kabul ediyoruz. Peki “daha iyi açıklamak” ne demek?
Yani önerilen $\mu$ ve standart sapma ile olabilirliği kullanarak, gözlemlerin olasılığını hesaplıyoruz. Bir nevi tepe tırmanma (hill climbing) algoritmasında olduğu gibi davranıyoruz. Yani rasgele yönlere atlamayı öneriyoruz, önerilerden hangisinin olasılığı güncel olasılıktan yüksekse o yöne atlamayı kabul ediyoruz. Eninde sonunda $\mu$’nün $0$ olduğu yere geleceğiz ve oradan başka yere zıplayamayacağız. Ama yine de sonuç olarak elimizde bir dağılım olmasını istediğimize göre arada sırada da $0$’dan uzak noktaları da kabul edeceğiz. Kabul ederken önerilen yerin olasılığını, güncel yerin olasılığına bölüyorduk. Çıkan orana bakarak kabul edip etmeyeceğimize karar veriyorduk.
Şimdi MZMC’nin koduna ve nasıl sonuçlar ürettiğine bakalım.
N = 100000
mu_guncel = 1.0
mu_oncul_mu= 1.0
mu_oncul_ss= 1.0
oneri_genislik= 0.2
sonsal = [mu_guncel]
nkabul = 0
for i in range(N):
# yeni konum öner
mu_oneri = norm(mu_guncel, oneri_genislik).rvs()
# olabilirlik hesapla (herbir gözlem noktasının olasılığını çarparak)
olabilirlik_guncel = norm(mu_guncel, 1).pdf(gozlem).prod()
olabilirlik_oneri = norm(mu_oneri, 1).pdf(gozlem).prod()
# guncel ve onerilen mu için öncül olasılıkları hesapla
oncul_guncel = norm(mu_oncul_mu, mu_oncul_ss).pdf(mu_guncel)
oncul_oneri = norm(mu_oncul_mu, mu_oncul_ss).pdf(mu_oneri)
p_guncel = olabilirlik_guncel * oncul_guncel
p_oneri = olabilirlik_oneri * oncul_oneri
u = np.random.uniform()
# öneriyi kabul olasılığını hesapla
r = p_oneri / p_guncel
#kabul?
if u<r:
# pozisyonu güncelle
mu_guncel = mu_oneri
nkabul += 1
sonsal.append(mu_guncel)
# sonsal dağılımı ve önerileri çizdir
if i==0 or (i+1)%(N/4)==0:
fig, (ax1) = plt.subplots(ncols=1, figsize=(4, 4))
x = np.linspace(-3, 3, 5000)
color = 'g' if kabul else 'r'
# sonsal dağılımı hesapla
sonsal_analitik = sonsal_analitik_hesapla(gozlem, x, mu_oncul_mu, mu_oncul_ss)
ax1.plot(x, sonsal_analitik)
sonsal_guncel = sonsal_analitik_hesapla(gozlem, mu_guncel, mu_oncul_mu, mu_oncul_ss)
sonsal_oneri = sonsal_analitik_hesapla(gozlem, mu_oneri, mu_oncul_mu, mu_oncul_ss)
ax1.plot([mu_guncel] * 2, [0, sonsal_guncel], marker='o', color='b')
ax1.plot([mu_oneri] * 2, [0, sonsal_oneri], marker='o', color=color)
ax1.set(title='iterasyon %i\nsonsal(mu=%.2f) = %.5f\nsonsal(mu=%.2f) = %.5f' % (i+1, mu_guncel, sonsal_guncel, mu_oneri, sonsal_oneri))
print ("Verimlilik = ", nkabul/N)
Bu algoritmayı çalıştırınca şöyle sonuçlar görmeye başlarsın.
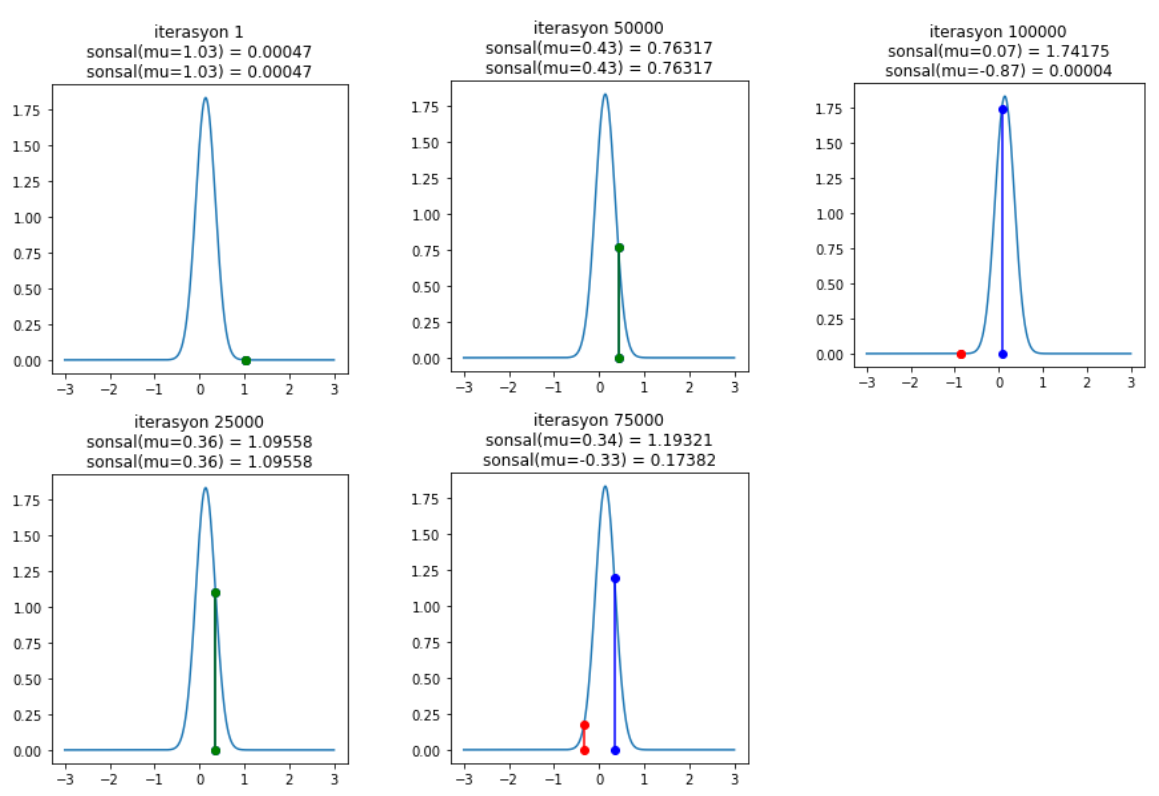
$75000$. ve $100000$. iterasyonda önerilen yerlerin nasıl reddedildiğine dikkat et. Gösterimsel olarak kalabalık olmasın diye her $25000$ adımda bir çizdiriyoruz ancak sen istersen her bir adımda kabul/reddin nasıl olduğunu incele. Sonuç olarak MZMC sonsal dağılımı buluyor ve en yüksek olasılığın $\mu = 0$ civarında olduğunu gösteriyor.
Simülasyonun sonunda hesapladığımız verimlilik önerilen örneklerin ne kadarının kabul edildiğini gösteriyor. Genelde %70’in üzerinde kabul edilmişse modelimiz doğru kurulmuş demektir. Bu simülasyonda %72 civarında kabul oranı çıkıyor ki bu da doğru yolda olduğumuzu gösteriyor.
MZMC ile elde ettiğimiz sonsal dağılımı analitik dağılımla karşılaştıralım.
import seaborn as sns
ax = plt.subplot()
sns.distplot(np.array(sonsal[500:]), ax=ax, label='sonsal kestirim')
x = np.linspace(-1.0, 1.0, 500)
sons = sonsal_analitik_hesapla(gozlem, x, 0, 1)
ax.plot(x, sons, 'g', label='analitik sonsal')
_ = ax.set(xlabel='mu', ylabel='güvenilirlik (inanç)');
ax.legend();
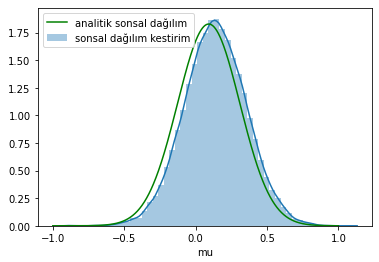
Kabul ettiğimiz $\mu$ değerlerinin histogramını hesapladık. Burada bir şey kafanı karıştırmasın. Sonuçta bulduğumuz dağılım da Normal dağılımdan örneklediğimiz gözlemlerin dağılımına benziyor ama bu bizim kestirimimiz. Başka bir modelde bambaşka bir dağılım da çıkabilirdi.
Gerçek Hayat
MZMC’nin bilinen iki problemi vardır.
- Başlangıç değerlerine bağımlılık
Birinci problemden kurtulmak için Zincir stabil hale gelene kadar ilk başta çektiğimiz örnekleri (ör; 500 tanesini) çöpe atabiliriz.
- Markov Zinciri’nin oto-korelasyonu
Markov sürecinin beklenen şekilde çalışması için bir durumun sadece kendinden önceki duruma bağımlı olması gerekiyor. Bir önceki durumdan öncekilere bağımlılık arttıkça MZMC’nin performansı azalacaktır.
Örneğin elde ettiğimiz sonsal dağılımın oto-korelasyonuna bakalım.
from pymc3.stats import autocorr
lags = np.arange(1, 30)
plt.plot(lags, [autocorr(np.array(sonsal), l) for l in lags])
plt.xlabel('lag')
plt.ylabel('oto-korelasyon')
plt.title('analitik sonsal dağılım')
plt.show()
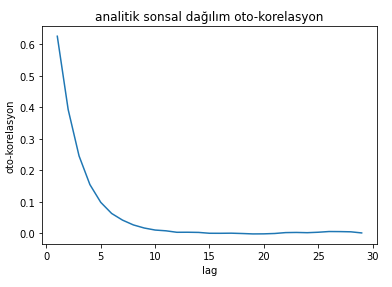
Figürden de görüldüğü özere $i+1$. örnek sadece $i$. örneğe bağımlı değil. Önceki örneklerle de güçlü bir korelasyon var. Bu problemden kurtulmak için de peşpeşe gelen örnekleri kabul etmek yerine her $n.$ örneği kabul edebiliriz. Buna Markov Zinciri literatürünce “inceltme” denilir. Örnek uzayı büyütülür ve her $n.$ örnek tutulur.
Sonuç olarak MZMC’yi kullanarak;
- model parametrelerinin sonsal dağılımı
- tahminlerin sonsal dağılımı
- model karşılaştırmasının sonsal dağılımını
elde edebiliriz.
Bu iki problem dışında Metropolis-Hastings’in de kendi içinde problemleri var. Örneğin MH’in seçtiği öneri dağılımı simetriktir. Gibbs Örnekleyici bu seçimi otomatikleştirmek için ortaya atılmış başka bir MZMC varyantıdır.
Diğer yandan MZMC’nin işlemsel yükü oldukça yüksektir. Bu nedenle literatürde algoritmayı paralelleştiren çalışmalara rastlayabilirsin.
Bir de önerilere bakarak nereye atlayacağını daha akıllıca yapan Hamiltonian Monte Carlo varyantı var. Onu da inceleyebilirsin.