Emre: Nedir abi bu Bayesçi çıkarım?
Kaan: Bir örnek üzerinden anlatabilirim.
Bayesçi çıkarım bir olasılıksal yaklaşımdır. Ne olduğuna dair biraz bilgi verebilmesi açısından doğrusal regresyon problemini ele alabiliriz. Şöyle ki, basit doğrusal regresyon yöntemi bağımsız bir değişkenin değerini temel alarak bağımlı bir değişkenin değerini tahmin etmek için iki değişken arasındaki doğrusal ilişkiyi analiz etmeyi sağlayan bir yöntemdir. Gerçek dünyada ve makine öğrenme problemlerinde bu ilişki genellikle istatistiksel bir ilişkidir. Ancak istatistiksel ilişkiler hakkında nasıl düşündüğümüzün özüne inmeden önce iki değişken arasındaki ilişkinin deterministik olduğu duruma bir göz atmamız lazım. Deterministik durumda, her zaman iki değişken arasındaki ilişkiyi kesin olarak tanımlayan mutlaka bir denklem vardır.
Problem
Örneğin, evden havaalanına gitmek için taksiye binmemiz gerektiğini düşünelim. Diyelim ki taksinin açılış ücreti olarak $7$ TL alacağını ve seyahat boyunca kilometre (Km) başına $0,8$ TL alacağınızı biliyoruz. Seyahatimizin toplam maliyetini bulmak için doğrusal bir denklem kurabiliriz. Eğer X kilometre biriminde kat edilen mesafeyi ve Y sürüşün toplam maliyetini temsil ederse, doğrusal denklem şöyle olur:
Denklemi deterministik olarak bildiğimiz zaman, aynı taksi hizmeti ile yaptığımız tüm seyahatlerin maliyetini tam olarak hesaplayabiliriz. Denklemi biliyorsak, veriler görselleştirildiğinde şöyle görünür:
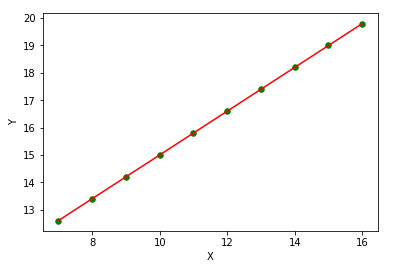
Klasik Doğrusal Regresyon
Şimdi bir de istatisiksel yaklaşımın nasıl olduğuna bakalım. Varsayalım ki bu kez yine taksideyiz, ancak bu sefer açılış ücretini ve Km başına ne kadar ücret alındığını bilmiyoruz, yine de daha sonraki seyahatlerimizin maliyetini hesaplayabilmek için taksimetrenin maliyet hesaplarken kullandığı doğrusal denklemi kestirmek istiyoruz. Bu durumda taksimetre ekranında gösterilen ücretin virgülden sonraki hanelerini görmezden gelerek sadece Km başına gösterilen maliyetin tamsayı kısmını bir yere not ettiğimizi varsayalım. Bu noktada görevimiz aşağıdaki denklemin parametrelerini bulmak için elimizdeki noktalara bir doğru uydurmaktır:
\[Y=\theta_{0} + \theta_{1} \ast X\]Aşağıdaki şekil, bu problem istatistiksel olarak çözüldüğünde, daha önce not ettiğimiz noktalara uyan doğruyu göstermektedir.
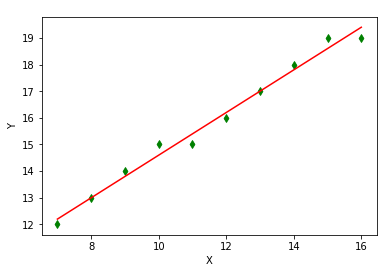
Tahmin ettiğimiz parametrelerin alacağı değerler şöyle olacaktır:
\[\hat{Y}=6.6+0.8 \ast X\]ki $\theta_{0}=6.6$ ve $\theta_{1}=0.8$ değerlerini alır.
Bir saniye, bu tahmini nasıl elde ettik?
Aslında doğrusal regresyon bağlamında en küçük kareler yöntemi literatürde geniş ölçüde ele alınmıştır. Dolayısıyla, algoritmanın detaylarına burada girmeyeceğim. Ancak hikayemizi inşa etmek adına, yöntemin bazı temellerini hatırlatmam gerekiyor.
Deterministik denklemi bilmediğimizi varsaydığımızdan, $Y$ değerlerini tahmin etmek için istatistiksel bir yaklaşım kullanacağız. Yapmamız gereken ilk şey, $X$ ile $Y$ arasındaki doğrusal ilişkinin ne olacağı hakkında elimizdeki tüm bilgileri kullanmak. Verilerin iki boyutlu bir düzlemde nasıl dağıldığına bakarak, bir eğri denkleminden çok bir doğru denklemiyle daha doğru ifade edilebileceğini görebiliriz. Bu durumda modelimiz şu şekilde olacaktır:
\[\hat{y_i} = \theta_0 + \theta_1x_i + \epsilon_i\]ki $\hat{y_i}$ burada $i.$ gözleme ait tahmini ve $\epsilon_i$’de $i.$ gözleme ait hatayı (ya da “artığı”) temsil etmektedir.
Eğer $\theta_0 + \theta_1x_i$ tahminini $\theta^Tx_i$ şeklinde ifade edersek, hata, gerçek değer $y_i$ ile tahmin $\hat{y}_i=\theta^Tx_i$ arasındaki fark olarak hesaplanır.
\[\epsilon_i= y_i - \hat{y_i}=y_i - \theta^Tx_i\]Hata terimi, bulmaya çalıştığımız doğrusal ilişki hakkında modelimizin açıklayamadığı kısmın bir ölçüsüdür. Doğrusal regresyonda amacımız, bu hatalarla ilişkili maliyet işlevlerini (Ortalama Mutlak Hata, Ortalama Kareler Hatası, Kök Ortalama Kareler Hatası, vs.) en aza indiren en uygun denklemi bulmaktır. Bu bağlamda, Artık Kareler Toplamı’nı (AKT) şu şekilde tanımlarsak:
\[g(\theta)= \sum_{i=1}^n(\epsilon_i)^2=\sum_{i=1}^n(y_i-\hat{y_i})^2=\sum_{i=1}^n(y_i-\theta^Tx_i)^2\]Problemimizin en az bir çözümü olan En Küçük Karelerle Uydurma yöntemi AKT’yı minimize etmeye çalışmaktadır:
\[J(\theta_1,\theta_2)=\underset{\theta_1,\theta_2}{\arg\min} \sum_{i=1}^n(y_i-\hat{y_i})^2=\sum_{i=1}^n(y_i-\theta^Tx_i)^2\]Emre: Bu denklemin yapmaya çalıştığı şey nedir?
Kaan: Farkların karelerini toplamak ve $\theta$ parametreleri üzerinden minimize etmek.
Emre: Neden kare alınıyor?
Kaan: Çünkü hatanın yönünü umursamıyoruz ve hataların toplanırken birbilerini iptal etmelerini istemiyoruz. Yine de umudumuz ve varsayımımız bu hataların ortalamasının (beklenen değer) sıfır olmasıdır. Bu, modelimiz hakkında yaptığımız varsayımlar açısından önemlidir. Her neyse, bu varsayıma geri döneceğim ve bunun neden önemli olduğunu daha sonra anlatacağım.
Emre: $\theta$ parametreleri üzerinden AKT’yi minimize etmek ne demek?
Kaan: Maliyet fonksiyonunun türevini alıp, türevi sıfıra eşitleyelim ve denklemi parametre vektörü $\theta$ için çözelim. Türevi sıfıra eşitleyen parametre değerleri aslında bize maliyet fonksiyonunun türevinin sıfır olduğu yeri yani maliyet fonksiyonunun mimimumunu verir. Bu aslında problemimizin kapalı form çözümüdür. Ancak alternatif olarak “Gradyan İnişi” algoritmasını da kullanabilirdik. Gradyan inişi algoritmasında konveks olan bir maliyet fonksiyonunun minimum noktası yine gradyan türevleri üzerinde yinelemeli bir yöntem izlenerek bulunur.
Emre: Bir dakika, “gradyan” tam olarak nedir?
Kaan: Gradyan her bir bilinmeyenin kısmi türevlerinin bulunduğu vektöre verilen isimdir.
Emre: Ne yapıyoruz bu türevlerle?
Kaan: Gradyan türevi bize mimimuma ulaşmak için hangi yönde gideceğimiz hakkında bilgi verir. Mesela, algoritma maliyet fonksiyonu üzerinde rastgele bir noktadan başlar, türev bize eğri üzerinde sağa mı sola mı gideceğimiz hakkında bilgi verir. Eğer türev negatifse sağa ilerler ve $\theta$’yı artırırız, pozitifse sola ilerler ve $\theta$’yı azaltırız. Bu işlemi ta ki minimum noktaya ulaşana kadar sürdürürüz. Minimuma ulaştığımızda türev sıfır değerini alacaktır. Sıfıra ulaşmayı beklemek yerine sıfıra yakın bir eşik değeri koyarak da algoritmayı erkenden sonlandırabiliriz.
Aşağıdaki şekil dışbükey bir fonksiyonda tek bir parametre için “Gradyan İnişi” yöntemi kullanılarak minimum noktaya nasıl ulaşılabildiğini göstermektedir.
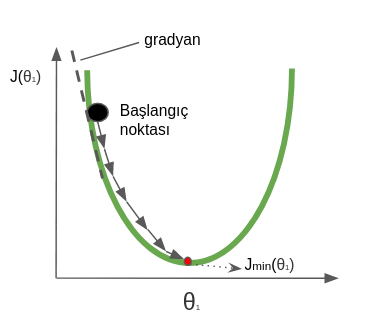
Öte yandan, örneğimizde sadece bir tane tahmin değişkeni $X_1$ ve iki bilinmeyen parametre ($\theta_0$, $\theta_1$) vardı. Gerçek dünya problemlerinde ise tahmin değişkenlerinin sayısı çok fazla olabilir. Örneğin kullanılmış araba fiyatlarını tahmin etmeye çalışıyor olsaydık, arabanın markası, modeli, kilometresi, güvenlik donanımı, vesair bir çok değişken olacaktı ki bu da problemi basit regresyon probleminden bir çoklu regresyon problemine dönüştürür. Bu durumda modelimiz artık şöyle olurdu:
\[\hat{y_i} = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + … + \theta_p x_p\]Bu artık bir doğrusal regresyon problemi değil “çoklu regresyon” problemidir. Böyle çok sayıda bağımsız değişkenli durumda yüksek boyutlar üzerinde çalışacağımız için artık türev almak oldukça zorlaşır, bu nedenle genellikle sürekli “gradyan” hesabı üzerinde çalışılır. Yine bir önceki örnekteki gibi, gradyan bir eşik değerinin altına düşünce yinelemeyi durduran bir yöntem kullanarak optimal nokta aranır.
Genel anlamda çoklu regresyonda gradyan aşağıdaki gibi ifade edilir:
\[\nabla J(\theta_1,...,\theta_p) = \begin{bmatrix} \frac{\partial J}{\partial \theta_0} \\ \frac{\partial J}{\partial \theta_0} \\ \vdots \\ \frac{\partial J}{\partial \theta_p} \end{bmatrix}\]Emre: Bütün bunların “Bayesçi Çıkarım”la ne ilgisi var?
İstatistiksel Yaklaşım
Kaan: Evet, şimdi gelelim doğrusal regresyon problemininin Bayesçi yaklaşımla çözülmesine. Problemi Bayesçi yaklaşımla çözebilmek için öncelikle problemi istatistiksel bir problem olarak düşünmemiz lazım.
Emre: Nasıl yani?
Kaan: Maliyet fonksiyonunu minimize eden bir “doğru uydurma” yerine, bu kez elimizdeki gözlemin olasılığını maksimize eden bir “doğru uydurma”mız lazım. Genel olarak, verinin nasıl oluştuğuna dair varsayımlarımızı kullanarak, elimizdeki verilerin olabilirlik fonksiyonunu şöyle hesaplayabiliriz:
\[L (olabilirlik) = p(y|x) = p(y_1|x_1,\theta)*p(y_2|x_2,\theta)...*p(y_n|x_n,\theta)\]Yukarıdaki olabilirlik fonksiyonu $L$’yi maksimize eden $\theta$ parametre değerlerini bulmak istiyoruz.
Emre: Bu formüldeki her bir olabilirliği ayrı ayrı nasıl hesaplayabiliriz ki?
Kaan: İşte burada yardımımıza Gauss dağılımı koşuyor. Hatırlarsan yukarıda hataların ortalamasının sıfır olduğunu varsaymıştık. Bir adım daha ileri gidip hata değerlerinin olasılık dağılımının Gauss dağılımına sahip olduğunu varsayalım.
Emre: Gauss dağılımı neye benziyor?
Kaan: Bizim meşhur çan eğrisi ya da diğer adıyla Normal dağılım. Hatırlayalım Gauss dağılımı şöyle ifade ediliyordu:
\[\mathcal{N}(\mu, \sigma^2)=\frac{1}{\sigma \sqrt {2\pi}}e^{-(x - \mu)^2 / {2\sigma ^2}}\]Ki burada $x$ rastgele değişkenimiz, $\mu$ ortalamayı ve $\sigma$ standart sapmayı temsil ediyor.
Şekil olarak neye mi benziyor?
$\mu=0$ ve $\sigma=1$ için görselleştirirsek şöyle görülür:
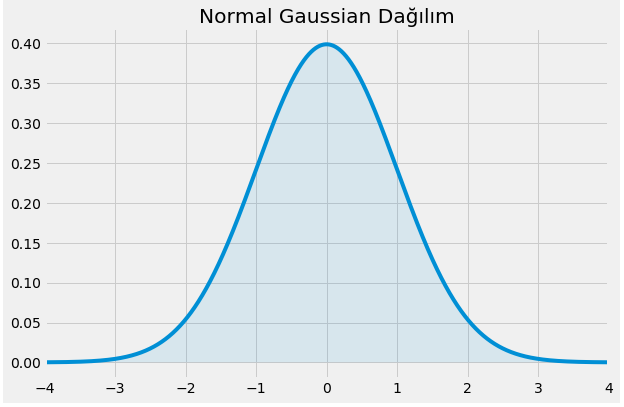
O zaman problemimizdeki hata olasılık dağılımını şöyle ifade edebiliriz:
\[\epsilon_i \sim \mathcal{N}(0, \sigma^2)\]Şimdi kaldığımız yere dönecek olursak, $L$ olabilirlik ifadesindeki her bir $p(y_i|x_i,\theta)$’yi nasıl hesaplayacağımızı düşünüyorduk.
Emre: $p(y_i|x_i,\theta)$ ifadesi bize ne anlatıyor?
Kaan: Şöyle, $x_i$ ve $\theta$’yı bildiğimiz durumda, $p(y_i|x_i,\theta)$ bize $y_i$ rastgele değişkeninin olabilirlik dağılımını ifade ediyor.
En başta ne demiştik,
\[\hat{y_i} = \theta_0 + \theta_1x_i + \epsilon_i\]Bu denklemde rastgele değişkenler sadece $y_i$’ve $\epsilon$ olduğundan, $y_i$’nin dağılımı aslında $\epsilon$ dağılımıyla aynı türdendir.
Lakin burada bir şeye dikkat etmek lazım. Dağılımların türü aynıdır ancak parametre değerleri farklıdır. $y_i$’nin dağılım parametrelerini bulmak için Gauss dağılımının bir özelliğinden yararlanabiliriz. Eğer $X=\mathcal{N}(\mu, \sigma^2)$ ve $Y=\mathcal{N}(0, \sigma^2)$ ise, o zaman:
\[X=\mu + Y\]denilebilir. Bu özelliği kullanarak ve $y_i=\theta^{T}x_i+\epsilon_i$ olduğunu bildiğimizden,
\[y_i~\sim \mathcal{N}(\theta^Tx_i, \sigma^2)\]diyebiliriz. Bu demektir ki, $y_i$ değişkeni de ortalaması $\theta^Tx_i$ ve varyansı $\sigma^2$ olan bir Normal dağılımına sahiptir. Böylece artık $L$ olabilirlik ifadesini $y_i$ rastgele değişkenlerinin olabilirlik dağılımlarının çarpımları cinsinden şöyle yazabiliriz:
\[L=\prod_{i=1}^n \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(y_i - \theta^Tx_i)^2}{2\sigma^2}}\]Eksponansiyel fonksiyonların $e^xe^y = e^{x + y}$ özelliğinden yararlanarak, L ifadesini şu hale getirebiliriz:
\[L=(\frac{1}{\sigma \sqrt {2\pi} })^ne^{-\frac{1}{2\sigma^2} \color{blue}{\sum_{i=1}^n(y_i - \theta^Tx_i)^2}}\]Emre: Neden ifadenin bir kısmı mavi?
Kaan: Sana yukarıda bahsettiğim bir şeyi hatırlatmadı mı?
Emre: Hmm, mavi olan kısım “artık kareler toplamı” ifadesinin aynısı değil mi?
Kaan: Aynen. Öyleyse, bu olabilirlik ifadesinin maksimumunu bulmak aynı zamanda artık kareler toplamının yani hatanın minimum olduğu yeri bulmaya denk geliyor değil mi?
Emre: Elbette. Yani istatistiksel yaklaşımda topladığımız verilerin olabilirliğini maksimize etmek aslında doğrusal regresyondaki artık kareler toplamını minimize etmeye denk geliyor.
Kaan: Çok iyi. İki yaklaşım arasındaki ilişki budur.
Emre: Peki Bayesçi yaklaşım işin neresinde?
Bayesçi Çıkarım
Kaan: Artık istatistik diliyle konuşmaya başladığımıza göre Bayesçi yaklaşıma nasıl ulaştığımıza bakabiliriz.
Bayes kuralını hatırlayalım:
\[p(A|B)=\dfrac{p(B|A)p(A)}{p(B)}\]Bu kural aslında B gözlemine (veya Bayesçi istatistikte sıkça kullanılan başka bir terminolojiye göre “kanıt”a) dayalı olarak $A$ olayının olma ithimaline dair koşullu olasılığı verir bize. Orjinalinde denklemin paydası daha karmaşık. Ancak burada paydaya basitçe $p(B)$ dedik. Bunun nedeni paydada aslında $B$ olayının tüm olasılıkları üzerinden $A$’nın hesaplandığı durumda $B$ olayının gerçekleşme olasılığının artık $A$ olayından bağımsız hale gelmesidir. Buna “marjinalleştirme” denilir. Bu durumda da $p(B)$ sadece sabit bir sayı olarak denklemde bir normalizasyondan başka bir şey yapmaz.
Yani şöyle desek yanlış olmaz:
\[p(A|B) \propto p(B|A)p(A)\]Bayes şu şekilde işlemektedir; bir hipotez hakkında önceden sahip olduğumuz bilgiler ışığında bir inancımız (ön yargı) vardır, sonra olay hakkında bazı yeni kanıtlar elde eder ve ardından da yeni kanıtlar ışığında bir sonsal inanca ulaşırız. Yani:
sonsal dağılım $\propto$ olabilirlik (kanıttan gelen bilgi) $\times$ öncül dağılım (ön yargı)
Özet olarak Bayesçi istatistikte sonuç temel olarak bir olasılık dağılımıdır. Yani noktasal tahminler yerine tahmini oluşturan olasılık dağılımları! Yani doğrusal bir modelin parametresi hakkında 5’e eşittir şeklinde bir hipotez yerine, ortalaması $5$ ve standart sapması $0.7$ olan normal dağılıma sahip bir parametreden söz edilir. Tahminleri noktasal olarak hesaplamaya çalışmak bir “Frekansçı” yaklaşımdır. Burada şunu belirtmeden geçemeyeceğim. İstatistik dünyası bu iki eksen etrafında kutuplaşır. Biri hipotezler hakkındaki ön bilgiyi belirli belirsiz kullanan Frekansçı yaklaşımken diğeri Bayesçi yaklaşımdır. Hangi aklı başında olan bir insana “analiz ettiğimiz bir olayla ilgili elimize yeni veriler geldiğinde inançlarımız mutlak doğru olan sonuca daha da yaklaşır, değil mi?” diye sorsanız, “evet” diyecektir. Bunu anlamak üstün zeka gerektirmez. Ancak asıl dahice olan bunu her koşulda matematiksel olarak ifade edilebilecek bir çerçeveye oturtmaktır. Bayes’in yaptığı da budur. Bayesçi yaklaşım ön yargıyı ve elimize gelen yeni verileri tutarlı ilkeler çerçeversinde ele alır. Biz de burada Bayesçi yaklaşım üzerinden gidiyoruz.
Yukarıdaki ifadede çoğu zaman denklemin sağ tarafındaki olabilirlik $p(B|A)$ gözlemleri üreten süreç tarafından belirlenir. Bu süreç hakkında da bazı varsayımlarda bulunmamız gerekir. Ama o detaya girmeyelim. Burada en çok dikkat edilecek husus şudur ki, Bayesçi yaklaşımın en önemli numarası son yargının (sonsal dağılım) bir sonraki tahmin için ön yargı (öncül dağılım) olarak kullanılmasıdır. Bunu aklımızın önemli bir köşesine not edelim!
Herneyse, asıl problemimizden çok uzaklaştık; bir adım geri dönelim. Bayes kuralı üzerinden artık öncül ve sonsal dağılımlar üzerinden konuşabiliriz. Bu durumda, bizim problemimizde de Bayesçi çıkarımı kullanmanın yolu önce her bir parametre için birer sonsal olasılık dağılımı hesaplamaktan geçer.
Herşeye rağmen, her parametre için bir sonsal olasılık dağılıma sahip olduğumuzda, tahminde bulunabilmek için parametrelerin sonsal olasılığı en büyük yapan değerlerini (Sonsal En Büyük Kestirim bkz. Maximum A Posteriori (MAP) Estimation) bulabilirdik. Böylece $\hat{y^{\ast}}$ tahminini şöyle yapabilirdik:
$\hat{y^{\ast}}$ = [$\theta_0$’ın sonsal en büyük kestirimi] + [$\theta_1$ ‘in en sonsal en büyük kestirimi]$x^{\ast}$
burada $x^{\ast}$, sonucunu tahmin etmek istediğimiz $\hat{y^{\ast}}$’ya ait daha önce görülmemiş yeni gözlemlerdir (yeni kanıtlar).
Kaan: Burada bir şey dikkatini çekmedi mi?
Emre: Ne kaçırdım?
Kaan: MAP kestirimlerini kullanmak bir “frekansçı” yaklaşım olurdu. Noktasal tahminleri istemiyoruz. Biz Bayesçi çıkarım yapmak istediğimize göre, parametrelerin olasılık dağılımlarını bulmalıydık! Bu nedenlere MAP kestirimlerine özel bir önem vermeyip yolumuza devam etmeliyiz.
Bu durumda her bir $x^{\ast}$ için, $y^{\ast}$’a ait birer olasılık dağılımı bulmalıyız. Bunun için modeldeki katsayıların, olası mümkün olan tüm doğrusal modelleri temsil eden ve her biri farklı bir $y$ tahminine denk gelen, sonsal olasılık dağılımlarını bulmamız gerekir. Böylece her bir olası doğrusal modelden gelen tahmin, o modellerin olasılıkları ile ağırlıklandırılmış olacaktır. Yani;
\[p(y^{\ast} | x^{\ast}, X, y) = \int_{\theta}p(y^{\ast} | x^{\ast},\theta)p(\theta|X,y)d\theta\]Bu formülde $X$ ve $y$’nin eğitim verisi olarak bize verildiğini varsayıyoruz. $x^{\ast}$ yeni gözlemleri temsil ediyor. Bu üç veriyi kullanarak $y^{\ast}$’u tahmin etmeye çalışıyoruz. Bunu yapmak için $\theta$ ‘nın sonsal olasılık dağılımları üzerinden bir marjinalleştirme yapmamız gerekiyor. Sonuç olarak elimizde varyansı $x^{\ast}$’in büyüklüğüne bağlı olan bir Gauss dağılımı kalıyor.
Burada karşımıza Bayesçi yaklaşımın bir güzelliği daha çıkıyor. Tahminleri bu şekilde elde edersek, elimizde her bir tahminin belirsizliği hakkında fazladan bir bilgi oluyor.
Emre: Her zaman bir şeyi bilmediğini bilmek en iyisidir!
Kaan: Aynen, aşağıdaki örnekte de görüldüğü üzere, gözlemlerden uzaklaştıkça yapılan tahminin hata marjini büyüyör (gri renkle gösterilen çizgiler her bir tahminin güvenilirlik aralığını gösteriyor). Bayesçi yaklaşım burada bize tahminlerimize ne kadar güvenebileceğimizi de söylemiş oluyor.
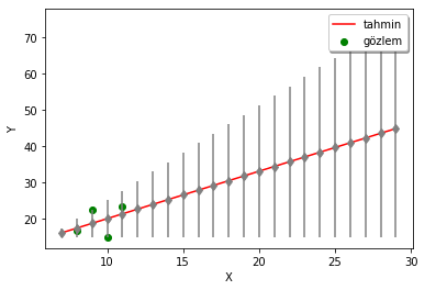
Özetle, doğrusal regresyon problemine her iki yaklaşım (Frekansçı ve Bayesçi) açısından da bakmış olduk.
İleri Seviye Konular
Daha da merak edenler için, pratik olarak Bayesçi çıkarım genellikle parametre kestirimi ve model karşılaştırma problemlerinde kullanılır. Çeşitli problem türlerinde Bayesçi olmayan rakiplerine (Maksimum Olabilirlik, Regülarizasyon ve BM (Beklenti-Maksimizasyon) göre Bayesçi yöntemler oldukça başarılı sonuçlar vermektedir.
Bayesçi çıkarım algoritmalarına örnek olarak Markov Chain Monte Carlo (daha da spesifik olarak Metropolis-Hastings) ve Varyasyonal Bayesçi Çıkarım gösterilebilir. Genellikle Bayesçi teknikler Gaussian Karışım Modeli (GMM), Faktör analizi ve Gizli Markov Modelleri (Hidden Markov Models) gibi üretken (generative) istatistiksel modellerle birlikte kullanılır. Bunun yanında yukarıda üzerinden geçtiğimiz gibi doğrusal regresyon modellerine de uygundur.
Gerçek Hayat
Bayesçi çıkarımın kullanıldığı istatistiksel problemler e-ticaretten, sigortacılığa, duygu analizinden metinlerde konu algılamaya, finanstan, sağlık sektörüne, borsadan, kendini sürebilen otonom araçlara kadar her alanda kullanılmaktadır. Bu nedenle makine öğrenmesi ile uğraşan herkesin basit düzeyde de olsa öğrenmesi gereken bir konudur.
Emre: Bence bu kadar yeter. Ara vermeden olmaz :)
Kaan: Peki o zaman, bir dahaki sefere ;)